Introduction
Stature estimation from the skeletal remains bears immense importance in the forensic sciences. Along with the conventionally used long bones, the humerus, femur, tibia, etc.; the ulna also has been used for the said purpose since 1952. Though studies which had highlighted the stature estimation in Bengalee males were carried on earlier, in females, this has still not been uncovered.
Objective
An attempt was made to formulate a linear regression equation for the estimation of the stature of living adult Bengalee females from the lengths of their ulna.
Method
This study was conducted in the Burdwan Medical College Hospital on 300 subjects who were chosen from among the patients and their lady attendants in the Gynaecology OPD. The height was measured from the crown to the heel and the length of the ulna was measured from the tip of the olecranon process to the tip of the styloid process. The documented data was calculated by the standard statistical software.
Result
The parameters were tabulated and statistically analyzed. The correlation coefficient (r) was found to be 0.82 (p=0.002) for the left ulna with stature and it was 0.67 (p=0.001) for the right ulna with stature. Supportive regression equations and scatter-plot diagrams could successfully interpret the height from the ulnar length in females.
Conclusion
The ulna being almost a percutaneous bone, it can be used for the prediction of the height. The ulna length provides an accurate and reliable means in estimating the height of an individual. The regression formulae which were proposed in this study will be useful for clinicians, anatomists, archeologists, anthropologists and forensic scientists when such evidence provides the investigator the only opportunity to gauge that aspect of an individual's physical description.
Introduction
The estimation of the stature (height) from different parts of the skeleton of the human body by anthropometric analysis is an area of interest to anatomists, anthropologists and forensic experts. The height of an individual, when it cannot be estimated directly, as in bedridden, old or frail patients, or in patients who have limb and/or vertebral column deformity; a indirect estimation can be achieved by correlating the height with other skeletal parameters. The ulna has easily identifiable surface landmarks which make the measurements possible in compromised postures, than in any other bones. Therefore, it can be utilized to formulate the height indirectly.
Pearson K, et al. (1898) [1] first introduced the co-relational calculus into the field of work for the prediction of the stature from the measurement of the long bones. Height is one of the factors in the description of impressiveness of an individual and it varies with race, age sex, heredity, climate and nutritional status. Telekka et al. (1950) [2] worked on the bones of the limbs and expressed the opinion that each racial group needs a separate formula for the estimation of stature.
Many of the previous workers worked on cadavers or on skeletal remains [3,4]. But cadavers cannot be the representatives of the population; because the cadavers are largely of persons who are aged, and they may have suffered from chronic debilitating diseases. It may be likely that they had been lying in an abnormal posture and it may not have been possible to straighten the body to get the accurate stature measurement. Again, according to Trotter M et al. (1952) [5], there is an increase in the height of 2.5 cm after death, when the measurement is taken in the recumbent posture.
Since over half of the century, the stature estimation has been linearly regretted with the length of the different long bones, especially for which the percutaneous measurement could be taken, like the ulna, the tibia, etc. The linear regression equation of the height on the ulna length has a definitive advantage over that of the tibial length, as it can be useful in the cases where the lower extremities are deformed, along with the deformities of the trunk [6]. Even the ulnar length was proven to be superior to the arm span measurement [7] and the hand length [8] in predicting the height.
Lundy JK (1985) [9] discussed the regression equation and the mathematical and the anatomical method of estimating the living stature from the long limb bones. The works of different researchers have postulated the linear regression of the height of an individual with the percutaneous ulnar length [10,11,7,12–15], both in the Indian and the international context. But till date, the data is quiet lacking for adult Bengalee females, as per the literature.
Objective
This study was based on research questions such as, ‘Can the height of an adult female be estimated from the percutaneous length of her ulna?’
Materials and Methods
This study was carried out in the purview of Burdwan Medical College Hospital, West Bengal, India, over a period of one year (January 2011 to December 2011); on 300 Bengalee females who were 20 to 50 years of age; who were chosen from among the patients and their accompanying persons who were waiting in the out-patients section of the Gynaecology Department. The patients of the 20-50 years age-group were approached, because the ulnar development and the ossifications complete by 20 years of age and as on the other hand, ladies who are above 50 years may have peri/post menopausal erosion in the bones.
Prior to the commencement of this study, the necessary permissions were taken from the institutional ethics committee as well as from the principal of the institution. The OPD used to be visited in the forenoon hours. The subjects who had any deformity/ailment in either of the upper limbs and those who did not give their consent for participation in the study, were not included in study. Informed consents were taken from each individual before including them as subjects in the study. The data collection was done more or less twice a week, which was spread over a period of 1 year.
The vertex to the heel height (in centimetre) was measured for each subject with them in the standing erect posture and also bare foot and they were asked to look forward straight to the horizon, so that the Frankfurt’s plane remained horizontal. A ruler was placed on their heads tangentially, so that it could touch the highest point of his/her head. Then, with the help of a pencil, that level was marked on the wall. With the measuring tape, the height of that point was measured from the floor level.
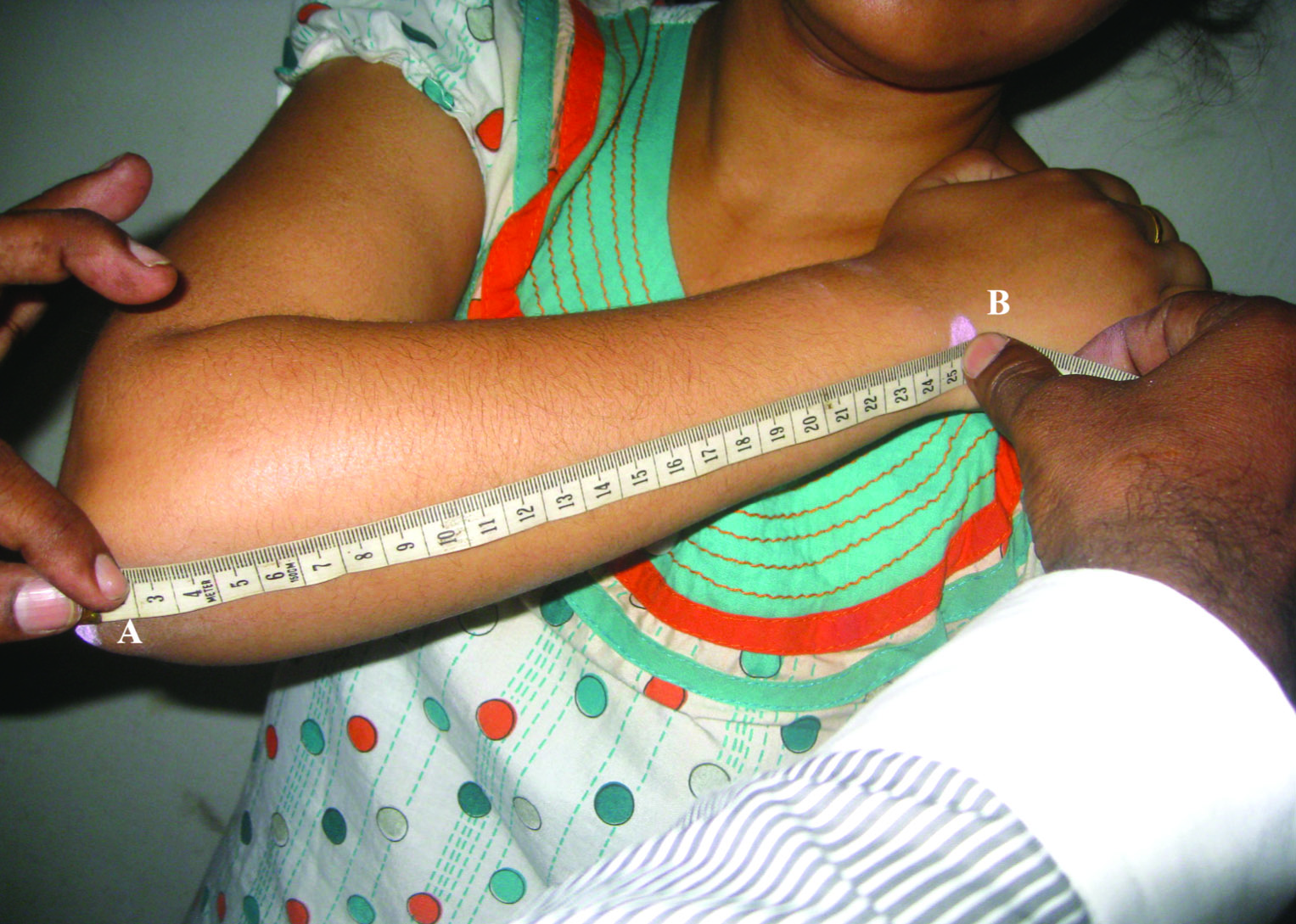
The ulnar length was measured from the tip of the olecranon process to the tip of the styloid process, with the elbow flexed and the palm spread over the opposite shoulder with the help of the same tape; on the right and the left sides consecutively [Table/Fig-1].
Estimation of height from length of left ulna in adult bengalee females (N=300)
| Independent variable | Dependent variable |
|---|
| Lt ulnar length (cm) | Height (cm) |
|---|
| Mean | 24.46 | 153.83 |
| Standard deviation | 1.18 | 6.32 |
| Correlation coefficient (r) | 0.82 [p=0.002] |
| Regression constant (a) | 45.89 |
| Regression coefficient (b) | 4.39 [p=0.0001] |
| Standard Error of estimate (STExy) | 3.59 |
Table shows different statistical outcomes showing inter-relationship of left ulnar length and height of a female individual.
The obtained values were used for the statistical analysis which was done by using the SPSS, version 12.0 software for the required analysis. The prediction of a significant relationship amongst the pair of variables was determined by the “Correlation coefficient” i.e., Pearson’s ‘r’. The relationship between the changes of a dependent variable (say, y) and an independent variable (say, x) was ascertained by simple linear regression, with the “Regression coefficient (b)”; where the model of the regression equation was y = a + bx [where a = y intercept, when x = 0]. As in every equation; a 95% confidence interval (which was equivalent to 1.96 standard deviation) was accepted and the standard error of regression (STE) was calculated. The final equation model was y = (a + bx) ± (1.96 x STE).
Result
The mean of the heights was extrapolated as 153.83cm, with a standard deviation of 6.32. Similarly, the means of the left and the right ulnar lengths were calculated as 24.46cm (with a Std. deviation of 1.18) and 24.55cm (with a Std. deviation of 1.17) respectively [Table/Fig-1, 2 and 3].
Figure showing the measurement of ulnar length in adult female subject. Tip of the olecranon process is marked as A and the ulnar styloid process is marked B. The length A→B demarcates the ulnar length.
Estimation of height from length of right ulna in adult bengalee females (N=300)
| Independent variable | Dependent variable |
|---|
| Rt ulnar length (cm) | Height (cm) |
|---|
| Mean | 24.55 | 153.83 |
| Standard deviation | 1.17 | 6.32 |
| Correlation coefficient (r) | 0.67 [p=0.005] |
| Regression constant (a) | 58.72 |
| Regression coefficient (b) | 3.89 [p=0.0002] |
| Standard Error of estimate (STExy) | 4.68 |
Table shows different statistical outcomes showing inter-relationship of right ulnar length and height of a female individual.
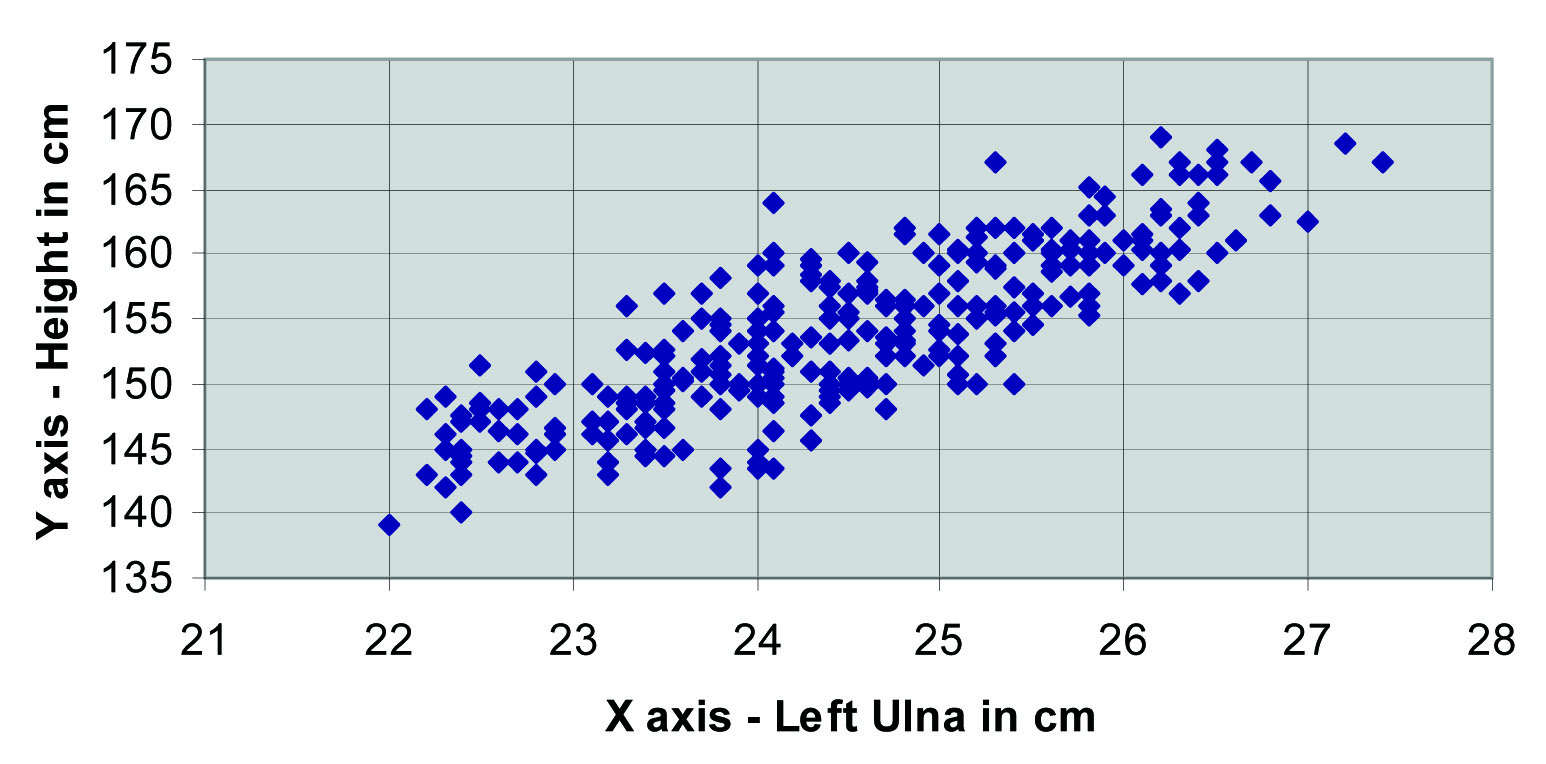
The correlation coefficient (r) of the height and the left ulnar length was 0.823 (p=0.002), with a significant regression coefficient (b) of 4.39 (p=0.001). A supportive regression scatter-plot can also be made [Table/Fig-1, Table/Fig-4].
Graphical representation of interpretation of height of an adult female from length of left ulna (N=300)
The graph shows showing inter-relationship of left ulnar length and height of a female individual.
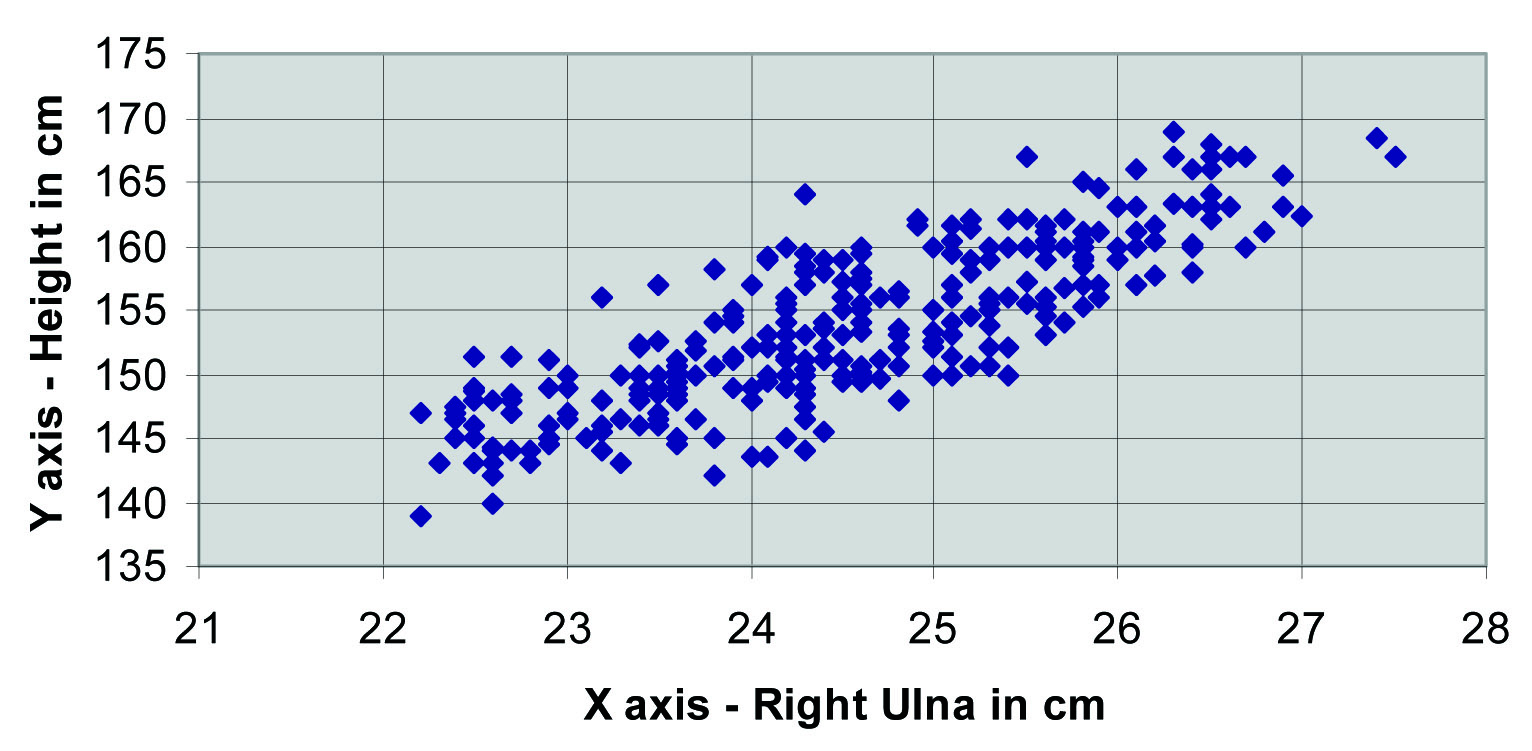
Similarly, the right ulnar length was also found to bear a significant correlation with the height of the individual, with a correlation coefficient of 0.67 (p=0.005) and a regression coefficient 3.89 (p=0.002) respectively. Here also, a supportive scatter-plot could be made, thus signifying the interpretation [Table/Fig-2, Table/Fig-5].
Graphical representation of interpretation of height of an adult female from length of right ulna (N=300)
The graph shows showing inter-relationship of right ulnar length and height of a female individual.
Thus, the regression equations became:
Estimated Height (cm) = 45.89 + 4.39 x Left ulnar length (cm) ± 7.03.
Estimated Height (cm) = 58.72 + 3.89 x Right ulnar length (cm) ± 9.17.
Discussion
In the present study, the correlation coefficient(r) of the height and the length of the left ulna was 0.82 and that for the right ulna was 0.67. The value of r implied that there was a positive correlation. This implied a significant contribution of the length of the ulna towards the height. The simple linear regression equation which has so far been derived can be used for the estimation of the height.
Our findings are at par with the findings of the previous researchers, as were reported in 1952. Trotter M et al., [5] estimated the stature of American whites and negroes from the ulna with linear regression equations. A study which was done by Lundy JK et al. (1985) [9] discussed the regression equation and the mathematical and the anatomical method of estimating the living stature from the long limb bones in the south African population. The reports of Agnihotri AK et al. (2009) [14] from Mauritius and those of Barbaosa VM et al. (2012) [15] from Portugal also found the linear regression model to depict an individual’s stature from the percutaneous ulnar length.
In India, Lal CS et al. (1972) [10] worked on a population of 258 in north Bihar, whose ages ranged from 12 to 21 years, for the estimation of the height from the surface anatomy of the long bones e.g. the tibia and the ulna. The ulnar mean multiplication factor was comparable in all the series. They claimed that the ulnar multiplication factor was a better guide for the calculation of the height, when it was not definitely known as to which part of the country the individual belonged. A similar study was done by Nath S et al., [11] in Delhi in 1990.
Devi S et al. (2006) [12] computed the correlation coefficient (r = 0.619 for males and 0.584 for females) and the regression equation formula for the estimation of stature by using the upper arm length among the living population of the Maring tribes of the Pallel area in the Chandel district, Manipur. In the Bengalee population, Mondal M et al. (2009) [13] postulated the height estimation in males from the ulna. The present study could highlight such a relationship in females.
Since the height of an individual progressively increases upto a certain age (till adolescence) and then decreases after a certain age due to vertebral column erosion, so the inclusion of a wider range of age groups could overcome its limitation for its applicability of the regression model. Moreover, a multi-centric approach in West Bengal will also supplement the findings in the Bengalee population in future. But still the regression formulae which are proposed will be of immense practical use in the clinical practice and in medico-legal, anthropological and archeological studies, where the total height of a subject can be calculated if the ulnar length is known.
Table shows different statistical outcomes showing inter-relationship of left ulnar length and height of a female individual.
Table shows different statistical outcomes showing inter-relationship of right ulnar length and height of a female individual.
[1]. Pearson K, A mathematical contribution to the theory of evolution. On the reconstruction of the stature of the prehistoric racesPhilos Trans R Soc. London 1898 Series A 192:169-244. [Google Scholar]
[2]. Telekka A, The prediction of the human stature from the long bonesActa Anatomica 1950 (9):103-11. [Google Scholar]
[3]. Mall G, Hubig M, Büttner A, Kuznik J, Penning R, Graw M, Sex determination and estimation of stature from the long bones of the armForensic Sci Int 2001 Mar1117(1-2):23-30.(available in http//:www.pubmed.gov. accessed on 23 June 2012) [Google Scholar]
[4]. Celbis O, Agritmis H, Estimation of the stature and the determination of sex from the radial and the ulnar bone lengths in a Turkish corpse sampleForensic Sci Int 2006 May10158(2-3):135-9Epub 2005 Jun 28. (available in http//:www.pubmed.gov. accessed on 23 June 2012) [Google Scholar]
[5]. Trotter M, Glesser GC, Estimation of stature from the long bones of American whites and negroesAm J Phy Anthropol 1952 (10):463-514. [Google Scholar]
[6]. Joshi NB, Patel MP, Dongre AV, Regression equation of the height from the ulnar lengthInd J Med Res 1964 52:1088-91. [Google Scholar]
[7]. Gauld LM, Kappers J, Carlin JB, Robertson CF, Height prediction from the ulnar lengthDev Med Child Neurol 2004 46(7):475-80. [Google Scholar]
[8]. Ilayperuma I, Nanayakkara BG, Palahepitiya KN, A model for the reconstruction of the personal stature, based on the measurements of the foot lengthGalle Med J 2008 13:6-9. [Google Scholar]
[9]. Lundy JK, The mathematical versus anatomical methods of stature estimation from the long bonesAm J Forensic Med Pathol 1985 6(1):73-76. [Google Scholar]
[10]. Lal CS, Lala JK, Estimation of height from the tibial and the ulnar lengths in north BiharJ Indian Med Assoc 1972 Feb1658(4):120-21. [Google Scholar]
[11]. Nath S, Krishan G, Determination of stature by using the percutaneous measurement of the upper and the lower limb bone among the Hindu females of DelhiJ Anthropol Survey Ind 1990 (39):151-66. [Google Scholar]
[12]. Devi S, Das H, Purnabati BK, Singh SD, Devi J, Estimation of stature from the upper arm length among the Marings of ManipurInd Med J 2006 Aug100(8):271-73. [Google Scholar]
[13]. Mondal M, Jana TK, Das J, Biswas S, Use of the length of the ulna in the estimation of stature in living adult males in the Burdwan district and in the adjacent areas of West BengalJ Anat Soc Ind 2009 58(1):16-19. [Google Scholar]
[14]. Agnihotri AK, Kachhwaha S, Jowaheer V, Singh AP, Estimating stature from the percutaneous length of the tibia and the ulna in an Indo-Mauritian populationForensic Sci Int 2009 May30187(1-3):109.e1-3.Epub 2009 Mar 14. (available in http//:www.pubmed.gov. accessed on 23 June 2012) [Google Scholar]
[15]. Barbosa M, Stratton RJ, Lafuente E, Elia M, Using the ulnar length to predict the height in English and Portuguese patient populationsEuropean Journal of Clinical Nutrition 2012 66:209-215.doi:10.1038/ejcn.2011.177; published online 12 October 2011 [Google Scholar]